
-
- Introducción.
La palabra sinergia está construida a partir de dos términos griegos, el prefijo sin, que significa con, y la palabra ergo, que significa trabajo. Así pues, sinergia significa trabajando juntos, cooperación. Por encima de las definiciones lingüísticas, esta palabra se construyó para designar los procesos físicos, químicos y biológicos donde todas las partes implicadas parecen trabajar para un fin común. Los resultados que se obtienen son siempre superiores a los que resultarían de la simple suma del trabajo aislado de cada una de las partes. Un ejemplo típico de sistema sinérgico son los organismos vivos, donde el trabajo de cada uno de los órganos es aprovechado por el cuerpo para mantenerse vivo y realizar sus actividades. Otro ejemplo sería cualquier máquina, donde la simple suma del trabajo de sus ruedas, bielas, pistones, por sí solo no obtiene nada pero acoplándolos se logra que la máquina funcione bien.
El lector puede pensar que lo anterior es una verdad de Perogrullo, y tendría razón, pero la inmensa diversidad de formas de la naturaleza y su perfecta funcionalidad hace que nos preguntemos de donde pueden salir tantas estructuras minerales, vegetales, animales, estrellas, planetas, etc. De la formación de estructuras muy complejas a partir de un estado más simple es de lo que se ocupa la sinergia. Para ello, como veremos, hace falta un gran aporte de energía exterior; nada es gratis en la economía del universo. Este nuevo enfoque permite contemplar el mundo como algo diferente, no compuesto de partes y reducible finalmente a éstas, sino como la interrelación hacia un objetivo común de todas las estructuras. Del conocimiento de las leyes generales que gobiernan la formación de estructuras surge un nuevo enfoque científico, la teoría general de sistemas, donde éstos ya no se contemplan como partes aisladas, sino que forman parte de una estructura común y sirven a una finalidad global y en un plano superior al sistema inicial.
Por otro lado, los fractales surgen como una nueva geometría, donde las formas de los distintos objetos naturales, tales como nubes, costas, montañas, ya no se explican como una combinación de líneas rectas, curvas, puntos, poliedros tridimensionales provenientes de la geometría euclídea, sino que dan nacimiento por sí mismos a una nueva geometría, donde lo irregular, lo fragmentado, lo caótico, tiene existencia por sí mismo. Asimismo la noción de continuidad, donde todas las partes de un cuerpo están unidas de manera que se puede pasar de una a otra sin saltos, sufre un duro golpe. Aparecen nuevas simetrías, invarianzas por cambio de escala y un nuevo concepto, el de autosimilitud.
Lo interesante tanto de la sinergia como de los fractales es que ambos surgen del estudio y la observación directa de la naturaleza. No es la naturaleza constreñida a unas leyes y contemplada de modo estático lo que ha dado nacimiento a estos dos nuevos enfoques, sino que el estudio directo de las formas y de la interacción de los sistemas ha sido lo que ha roto viejos prejuicios y ha permitido que aparezcan estas dos nuevas formas de enfocar la ciencia. Ambos han terminado por dar muerte al reduccionismo y al simple análisis de parte. Ambos han dado nacimiento a la visión de un mundo global, donde todas las cosas interrelacionan entre sí.
-
- Acción en conjunto. Interrelación
A la hora de tratar de comprender la naturaleza, tradicionalmente se ha empleado el análisis de partes. Consiste en analizar un sistema, descomponerlo en sus partes fundamentales y estudiar cada una por separado. Esta es la esencia del conocido como método científico. Sin embargo, esta visión reduccionista ha recibido un duro golpe a lo largo del siglo XX. La aparición de teorías como la relatividad, la mecánica cuántica o la teoría del Caos han dejado claro que el análisis de partes tiene un límite, y una vez pasado éste resulta mejor enfocar el estudio de sistemas completos y su interrelación común. Este es precisamente el método de la sinergética que no se ocupa de las diversas reglas elementales, sino de las leyes generales que rigen la formación de las estructuras, observando los modelos finales que se forman al terminar el proceso. Veremos que hay una serie de caminos inevitables para todo sistema que quiera crecer y formar nuevos modelos. En el tránsito hacia esos modelos veremos como las partes de un sistema aprenden a cooperar entre sí, como si estuviesen al servicio de un plan común, de una inteligencia que regula las formas y que las encamina hacia su finalidad. Así se obtiene uno de los viejos sueños de la ciencia, una cosmovisión, una concepción única del mundo.
Además lo más interesante de este nuevo enfoque es que se puede aplicar también a las ciencias sociales. Esta visión del individuo integrado en una sociedad y a su vez la presión social sobre el individuo permite una liberación mutua de esfuerzos hacia un fin común. Por ejemplo, en el planteamiento de las teorías económicas se estudia el comportamiento de grupos muy elevados de individuos y como interaccionan entre sí. Eso permite realizar predicciones, estudiando al mismo tiempo las interrelaciones entre los individuos aislados, y como en el seno social aparece una idea que domina la sociedad en la que se gestó. En el mundo empresarial sucede que de repente los directivos de empresas distintas y en competencia comienzan a aplicar la misma estrategia. Ello se debe a que una idea innovadora es aplicada por una empresa, y por imitación, que es uno de los conceptos fundamentales de la sinergia, el resto de empresas siguen ese comportamiento.
Un ejemplo social de sistema sinérgico fue la aparición de la Gran Depresión del 29 en los Estados Unidos, donde se impuso la idea de una venta masiva de acciones, lo que provocó una demanda de liquidez que colapsó el sistema financiero. O previamente los felices años 20, donde todas las empresas cotizaban al alza de una manera desmesurada. Vemos como un comportamiento colectivo se impone a un sistema aparentemente aislado de individuos. Otro ejemplo más triste lo tenemos en la ola de antisemitismo que azotó la Alemania de los años 30 del pasado siglo, donde se culpabilizó a los judíos de casi todo lo malo. Se piensa que esa ola fue provocada por Hitler, pero este lo que hizo fue potenciar a través de la propaganda una idea que ya estaba latente en el seno social y que simplemente esperaba ser activada.
Muchos otros ejemplos de sinergia se pueden aplicar, pero todos ellos se caracterizan por un conjunto de individuos que sirven a una idea global dominante y aglutinadora en un esfuerzo común. Esta es la idea básica de la sinergia.
-
- Ejemplos prácticos de sinergia.
 El láser
El láser
¿Qué es un láser? Básicamente es algo muy extraño en la naturaleza, es un halo de luz monocromática prácticamente puro. Generalmente la luz que recibimos (y no sólo la luz visible, todas las radiaciones electromagnéticas desde las ondas de radio, los infrarrojos, llegando hasta los ultravioletas y los rayos X), está compuesta de una longitud de onda predominante, que es la del color que podemos percibir, pero al mismo tiempo acompaña a esa longitud dominante otras radiaciones menos intensas pero que también contribuyen a la energía de la onda dominante. Es como un ovillo de hilos de distintos colores, donde estuviese uno en mayoría, pero los demás también están presentes y contribuyen al tono. Así, visto desde lejos el ovillo parece de un color, pero al acercarnos se resuelven los distintos tonos. Lo mismo sucede con un rayo normal de luz.
Sin embargo, en el láser observamos un rayo de luz monocromática, un tren de ondas totalmente regular. ¿Cómo aparece un láser? Surge porque una longitud de onda inicial se realimenta en todo el sistema hasta que todos los átomos vibran conjuntamente en esa longitud de onda (o frecuencia, ya que son conceptos recíprocos). Se estimula la emisión de radiación electromagnética en los átomos, y mediante dos espejos se impide que la luz salga de la lámpara de descarga. Con eso se consigue que el sistema se realimente a sí mismo un número enorme de veces, hasta que la onda principal domina todo el sistema. En ese momento se deja escapar una pequeña parte, que es lo que conocemos como láser. Los átomos son poseídos por una forma de vibración que hace que emitan un solo rayo de luz monocromático. Pero al mismo tiempo debemos saber que los átomos no vibran en cualquier frecuencia, sino que una específica es la que los armoniza globalmente. Así, no cualquier rayo puede ser láser, sólo aquel que sea preferentemente aceptado por los átomos.
Vemos aquí un ejemplo de sinergia. Los átomos individuales son forzados a cooperar en una tarea común, una emisión de láser. Esa fuerza al mismo tiempo debe tener afinidad química o física con cada átomo en particular. El sistema entero coopera en un objetivo común que le es afín. El sistema entero se comporta como una unidad.
La gran ola
En 1838 el ingeniero escocés John Scott Russell observó en los canales de Escocia la formación de algo antes nunca visto. Al contemplar el desplazamiento rápido de una barcaza y su brusca detención, pudo ver como una gran masa de agua de pronto se ponía en movimiento, continuaba a lo largo del canal sin dispersarse y tomaba la forma de un gran montículo redondeado, a la manera de una ola pero que no se disipaba en su movimiento a través del canal. Tras perseguirla durante más de un kilómetro la ola se perdió en las vueltas y desvíos del canal, pero sin perder en ningún instante su forma.
Normalmente una ola se desintegra a los pocos instantes de ser formada, salvo que la perturbación que le dio nacimiento se mantenga. Así, la formación de olas en la playa se debe al choque con el fondo poco profundo. Las grandes olas de las tormentas se formas gracias a los movimientos muy veloces de grandes masas de aire, pero al poco tiempo se disipa. Podemos imaginar la sorpresa del ingeniero escocés, cuando observó que su ola no se disipaba, sino que continuaba moviéndose como si una influencia oculta la mantuviese. Pero esa influencia oculta no era sino el acoplamiento global de las pequeñas olas individuales que habitualmente se forman. Este fenómeno después ha sido observado multitud de veces y no sólo en sistemas acuáticos, sino también en las nubes. Remolinos de agua condensada se forman pero en lugar de cambiar continuamente mantienen su forma global durante mucho tiempo, alimentándose de las corrientes aéreas y de nuevas nubes que absorben. Un ejemplo típico de esto se puede ver en otro planeta, Júpiter. La Gran Mancha Roja se cree que puede ser una inmensa gran ola que domina un hemisferio y que se alimenta de corrientes gaseosas que circulan a lo largo del planeta. Su existencia, por lo menos es de más de 300 años, desde que se observa Júpiter al telescopio.
Estas grandes olas se conocen con el nombre de solitones, y se han observado incluso en los fenómenos cuánticos, de migración de energía a través de los metales. Normalmente la energía que se aplica a un cuerpo se distribuye uniformemente a través de él, lo que se conoce como el principio de igualdad de división de la energía. Cual no sería la sorpresa cuando en los años 50 Enrico Fermi y dos matemáticos rusos observaron como en un metal que presentaba 5 modos de vibración distintos éstos no se daban simultáneamente según su probabilidad mutua, sino que durante un tiempo predominaba uno, luego el siguiente, y así, como si toda la energía se concentrase en un solo modo de vibración y luego pasase al siguiente, como si la energía no se dispersase, sino que viajaba como un solitón a través de los distintos modos de vibración.
La formación de esta ola autoorganizativa responde a los principios de la sinergia. Todas las ondas individuales se acoplan en una común que se ve multiplicada hasta observarse macroscópicamente. Para ello es necesario que la energía en juego sea la correcta, ni demasiada porque el fenómeno degenera en turbulencia, ni demasiada poca que no pueda acoplar todo el sistema. Una idea global, la adecuada, es la que domina el sistema y lo pone a su servicio.
La hipótesis Gaia
Quizás el mejor ejemplo de sinergia lo encontremos en la teoría desarrollada por el químico James Lovelock, la hipótesis Gaia. Según esta hipótesis, todas las especies de la tierra están coevolutivamente coordinadas de tal modo que nuestro planeta es una estructura globamente considerada, como si fuese un gigantesca célula única, un organismo vivo. La idea básica es que la vida crea las condiciones para su propia existencia. No es algo que haya surgido por azar de la “sopa orgánica” que postulan los científicos para los primeros tiempos de la tierra, sino algo que existía desde el comienzo y que, poco a poco, en inmensas escalas de tiempo, ha ido generando las especies y las condiciones para que todos los seres vivos puedan evolucionar conjuntamente, como si todos formasen parte de un organismo común. Naturalmente, esto implica una escala cósmica en la evolución de la Naturaleza. Precisamente la interrelación y la autosimilitud entre lo pequeño y lo grande es una de las principales ideas que dominan tanto en la sinergia como en los fractales.
¿Cómo llegó Lovelock a postular la existencia de Gaia? En los años 70 Lovelock recibió el encargo de la NASA de que idease un modo de detectar vida en Marte. Lovelock inmediatamente se puso a trabajar sobre como se podría detectar desde el espacio exterior si había vida en la tierra. Lo primero que le llamó la atención fue la composición de la atmósfera terrestre, ya que ésta no se hallaba en equilibrio químico, sino que para poder mantener esa composición debería existir un factor externo que desequilibrase el sistema y lo alejase del equilibrio, manteniéndolo en su composición actual. Ese factor desequilibrante era la Vida. Por contraparte, la atmósfera marciana se halla en equilibrio químico, no existe ningún impulso que lo aleje del equilibrio, con lo cual dedujo acertadamente que la existencia de vida en Marte era imposible, por lo menos a escala planetaria.
Lovelock fue colaborador de la microbióloga Lynn Margulis, y para esta bióloga la idea básica es la de cooperación en lugar de competencia, las especies cooperan entre sí para lograr evolucionar, en lugar de competir entre sí y eliminarse en la lucha por la vida. Margulis lleva la idea de cooperación, de sinergia, un poco más allá. Para ella el individuo aislado de su entorno es una abstracción, una mera categoría mental que hemos inventado nosotros. Y precisamente la tendencia de la naturaleza es precisamente a evolucionar trascendiendo todas las categorías. Margulis señala que para poder superar la crisis ambiental, ecológica y social que nos amenaza hemos de descubrir formas de cooperación y de acoplamiento social totalmente nuevas. De nuevo se busca una unidad global que antes sólo aparecía en las religiones orientales. Es la idea básica de la sinergia la que aparece de nuevo.
-
- Las dimensiones fractales. La paradoja de la longitud y la continuidad
En un artículo ya clásico, Benoit Mandelbrott, el genial matemático descubridor de los fractales, se pregunta ¿cuánto mide la costa de Bretaña? Es una pregunta bastante simple, bastaría con consultar un mapa, colocar un hilo alrededor de la costa, siguiendo el trazo de la isla, y con medir el trozo de hilo y aplicar la escala del mapa ya lo tenemos. Fácil, ¿no? Bien, si cambiamos a un mapa con una escala menor, de 1:50.000 a 1:10.000, es lógico pensar que ahora el trozo de hilo recogerá más detalles, y la longitud total medida será mayor. Podríamos seguir reduciendo la escala del mapa, y los resultados medidos cada vez serían más elevados. Incluso, si fuésemos ricos y ociosos, podríamos encargar el trabajo a un topógrafo, y decirle el margen de escala que debe tomar en su labor, por ejemplo, de 200 metros, de 100 metros, etc. Conforme menor sea el margen de error que le permitamos, la longitud medida será mayor, ya que se tomarán en cuenta cada vez más recovecos y promontorios. Finalmente, si tomase en cuenta todas las piedras, las rugosidades de las piedras, el perímetro de cada grano de arena, la longitud de las moléculas y las estructuras cristalinas de los minerales, cada distancia interatómica, etc., se hace obvio que el resultado de la medición será infinito.
¿Dónde está el fallo?, se preguntará el lector. El problema es que no hay fallo. La distancia entre dos puntos, si la queremos medir con una precisión cada vez mayor, aumentará cada vez más, hasta que sea infinita. Fíjense en que el resultado es válido no sólo para la costa de Bretaña, sino para cualquier isla, cualquier frontera entre dos países, cualquier distancia topográficamente medida. Además, sacamos como consecuencia que si queremos medir algo siguiendo un número finito de pasos, el resultado obtenido dependerá del observador, ya que éste decide donde quiere detener su recogida de datos, así como el patrón a utilizar. Esta es una conclusión muy parecida a la descrita en mecánica cuántica, donde el observador y lo observado forman una trama cuántica inseparable, en la que ambos están integrados en una realidad macroscópica global. Así, nuestro punto de vista se hace ilusorio, ya que depende de la realidad global en la que nos integramos. Lo pequeño influye sobre lo grande, y viceversa. Si bien es cierto que para tratar de cuantificar superficies y fronteras como las anteriores se ha recurrido a la dimensión fractal, ello no es más que un patrón de orden que elegimos para tratar de explicar algo totalmente extraño a nuestros sentidos y nuestra percepción cotidiana.
Quizás el gran problema está en que usamos conceptos abstractos, tales como punto, línea, distancia, etc., que están totalmente simplificados, no tienen realidad en sí. Son simples patrones mentales que nos inculcaron a través de la educación, y que seguimos usándolos, muy a menudo sin preguntarnos qué son realmente. Por ello caemos en paradojas como las anteriores, porque la mente creadora de ideas abstractas en sí es paradójica. Es paradójica la idea de la longitud entre dos puntos, porque está basada en la noción de continuidad, algo que es un postulado aceptado pero no probado, y que cuando se lleva a sus últimas consecuencias produce paradojas.
Hace falta entonces un nuevo enfoque geométrico, y ese nuevo enfoque lo aportan los fractales. Para medir los fractales se utiliza un generador y un módulo de repetición, y como consecuencia el concepto de dimensión se rompe, aparecen números fraccionarios para medir dimensiones de objetos fractales, cuando lo habitual en la geometría euclídea era el uso de números enteros, 1 para la línea, 2 para el plano, 3 para el espacio, y números más grandes para dimensiones superiores que no podemos visualizar pero que podemos realizar cálculos con ellas. Así, este simple enfoque se rompe cuando se nos dice que, la longitud de la costa de Bretaña es de 1,26, que es superior a una línea pero inferior a un plano. De ahí el nombre de fractales. Lo irregular, lo fragmentado, lo caótico, toma el poder. Sin embargo, debido a que nacen de un módulo que se repite infinidad de veces, están sujetos al concepto de autosimilitud.
-
- Autosimilitud. El número de oro.
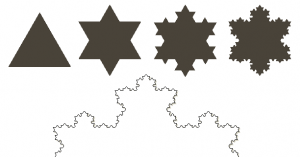
La principal característica de los fractales es la autosimilitud, cada parte de un fractal refleja la estructura global en la que encaja, y al revés, la estructura global del sistema se repite en cada una de sus partes, por diminuta que sea. Esto, a primera vista, parece una locura. Y sin embargo así sucede. Si observamos la curva de la matemática sueca Von Koch, que surge cuando extraemos de los lados de un triángulo su parte central y la sustituimos por otros dos lados formando un nuevo triángulo, y así lo repetimos infinidad de veces, vemos que si el proceso se repite hasta el infinito tenemos una estructura autosimilar en todas sus partes. Debemos recordar que esta figura la recreó Von Koch en 1904, así que la historia de los fractales viene de lejos. Esta curva tiene dimensión fraccional, concretamente su valor es de 1.2619, entre una línea y un plano. Cada parte de la misma es igual al todo, y viceversa. Podemos pensar que un patrón ha ordenado todo el sistema haciéndolo repetir en lo pequeño y en lo grande la misma forma. Es la misma idea que aparece en la sinergia. Todo ello le otorga unas propiedades muy curiosas. Por ejemplo, la longitud de la curva es infinita, ya que en cada paso la longitud sube a 4/3 de la inicial. Sin embargo, el área encerrada por la curva es sólo de 9/7 veces la del triángulo del comienzo. Al imponer la idea de autosimilitud y de invarianza por cambio de escala aparece estas aparentes contradicciones, ya que están basadas en ideas que en el fondo no son naturales, como la línea, el plano, curvas contínuas, etc.
Las ideas de autosimilitud y de invarianza por cambio de escala no son nuevas. Aparecen en los escritos de algunos filósofos al referirse a la formación del universo. Veamos el siguiente pasaje del Timeo de Platón.
[…]Pero no es posible unir bien dos elementos aislados sin un tercero, ya que es necesario un vínculo en el medio que los una. El vínculo más bello es aquél que puede lograr que él mismo y los elementos por él vinculados alcancen el mayor grado posible de unidad. La proporción es la que por naturaleza realiza esto de la manera más perfecta. En efecto, cuando de tres números cualesquiera, sean enteros o cuadrados, el término medio es tal que la relación que tiene el primer extremo con él, la tiene él con el segundo y, a la inversa, la que tiene el segundo extremo con el término medio, la tiene éste con el primero; entonces, puesto que el medio se ha convertido en principio y fin, y el principio y fin, en medio, sucederá necesariamente que así todos son lo mismo y, al convertirse en idénticos unos a otros, todos serán uno. (Páginas 168 y 169 del Timeo de Platón en la edición de Editorial Gredos de 2000).
Es posible que el lector haya reconocido la proporción áurea o el número de oro, proporción que por su belleza y simplicidad ha sido usada como patrón en las artes plásticas y que además aparece en la naturaleza, desde la espiral de la concha del Nautilus hasta el apilamiento de pétalos en las flores siguiendo la sucesión de Fibonacci, cuyo cociente entre dos términos sucesivos tiende al número de oro.
Así pues, el número de oro es el padre del concepto de autosimilitud, que es la principal característica de los fractales. La filosofía y las matemáticas se dan la mano. La ciencia tradicional y la nueva ciencia caminan juntas, lo pequeño y lo grande se relacionan por sinergia (trabajo en común) y por autosemejanza (fractales).
-
- Fractales en la naturaleza.
Los fractales no dejarían de ser una simple curiosidad matemática si no fuese porque las formas que usa la naturaleza para sus cuerpos son invariantes por cambio de escala. El caso típico es la ramificación de un árbol; del tronco a las ramas mayores y siguiendo a las menores y llegando a las hojas se repite el mismo tipo de esquema. Lo mismo sucede en los ríos, donde el río principal y sus afluentes repiten el mismo esquema, conforme vamos remontando y siguiendo el cauce y sus ramificaciones, etc. Veamos algunos ejemplos, que una imagen vale más que mil palabras.
Otro caso lo encontramos en el perfil de una montaña. Tradicionalmente los topógrafos sabían que el perfil general de una cordillera se repetía en sus partes más pequeñas, hasta llegar a los accidentes del terreno. Es lógico suponer que si las fuerzas de la erosión actúan modelando el terreno a gran escala, la misma forma se repita a escala más pequeña, ya que siguen actuando las mismas fuerzas.
El ejemplo de fractal natural más fácil de observar lo encontramos en las nubes; una observación atenta de las mismas refleja el mismo esquema tanto en lo grande como en lo pequeño. La misma forma se repite un número indefinido de veces. De nuevo debemos esperar que sea así, ya que están sometidas a los mismos fenómenos atmosféricos, y deben reflejar esa influencia en todos sus detalles.
Para finalizar, habría que hacer hincapié en la idea de que tanto la sinergia como los fractales son dos aspectos de la misma idea. Esa idea actúa como un patrón sobre la naturaleza informe, organizándola y dejando su huella en todos los lugares. ¿Hay algo más hermoso que poder reconocer el universo en un grano de arena?





















