Dicen que el ser humano es científico, es poeta y es filósofo al mismo tiempo, y que es capaz de descubrir las leyes de la Naturaleza, la Verdad, y la Belleza.
Las matemáticas tienen una Belleza especial, la atemporalidad. Una verdad matemática se mantiene a través del tiempo y no es necesario revisarla, recomprobarla una y mil veces, tiene vocación de eternidad. Por ejemplo:
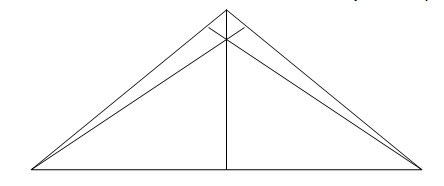
“Las tres alturas de un triángulo se encuentran en un punto ¹ (Altura es la perpendicular trazada desde un vértice hasta el lado opuesto)”.
A primera vista no vemos la razón por la que esto deba ser así. Tres rectas cualesquiera no tienen por qué converger en un punto, en general forman un triángulo. Es sorprendente, o como mínimo curioso que esta verdad geométrica se cumpla siempre, en cualquier país del mundo, tenga el régimen político que tenga, y en cualquier época de la historia.
Otro ejemplo de la matemática aritmética: “Sumando los números consecutivos impares empezando por el uno (1+3=4; 1+3+5=9; 1+3+5+7=16) obtenemos siempre cuadrados perfectos ².”
– ¿Y no es bella esta ley tan sencilla?- preguntamos y afirmamos a la vez.
– “Sí, pero poco útil” – puede argumentar nuestro sentido utilitarista de civilización occidental y moderna.
– Quizás la Belleza matemática no la podamos vender o comprar, pero será Verdad siempre, y será un punto en común para la inteligencia humana a través de los siglos.
Spinoza: “Es propio de la naturaleza de la Razón percibir las cosas bajo una cierta especie de eternidad”.
¹ La demostración de este teorema se puede encontrar en cualquier libro de geometría básica.
² Números que pueden obtenerse mediante el producto de otro por sí mismo (2×2=4, 3×3=9, 4×4=16,…)





















