
La vida es un tratado de matemáticas. Ya los antiguos y los estudiosos de todas las épocas descubrieron que la naturaleza, en su manifestación en infinidad de formas de vida, se rige por leyes de carácter matemático. Algunos llegaron más lejos, y descubrieron que son las relaciones matemáticas las que nos hacen percibir la belleza en las formas, lo cual permitió a algunos maestros plasmar estas mismas leyes en sus obras de arte.
Impulso vital y crecimiento armonioso
Es conveniente recordar en el simbolismo antiguo la estrella de seis puntas, donde espíritu y materia se unen en dos triángulos equiláteros de sentido contrario, el uno blanco y el otro negro, armonizados por un punto central. Un equilibrio perfecto para los antiguos sabios, que emplearon esta figura para simbolizar el macrocosmos como universo ordenado (Natura-Naturanda) y en cuyo interior dibujaban el símbolo del microcosmos, la estrella de cinco puntas. La belleza de la naturaleza, en su enorme variedad de formas, sigue tal vez procedimientos muy sencillos, en busca de un equilibrio y un orden.
En cambio, sucede algo diferente cuando los organismos que se analizan dominan el equilibrio estático y crecen o se desplazan venciendo la gravedad y la inercia de la materia; tal es el caso de los vegetales, los animales y el ser humano. La formas geométricas que predominan ya no son tan simétricas. Al contrario que en los minerales, el crecimiento no es por aglutinamiento o presión exterior, sino que es el producto de una expansión desde el interior, de dentro hacia fuera. Por esta razón, en algunos organismos primitivos predominan formas esféricas, buscando todavía la mínima superficie y el máximo volumen, por ejemplo un huevo. Pero en general, tienen la particularidad de poseer un solo plano de simetría, que es paralelo a la dirección del movimiento o el crecimiento, conservando las líneas generales de su forma.

La ley de ahorro de materia y energía sigue presente, pero de otro modo. Hay una necesidad de evolución que impulsa la vida orgánica a su desarrollo, ya no obedece a las líneas geodésicas de crecimiento estacionario. Esta tensión de fuerzas contrarias da como resultado otros patrones en los que predomina la geometría pentagonal y el tema asimétrico de la sección áurea. Esa economía de sustancia es realizada con éxito por plantas, aves y animales veloces. Es la lucha contra la gravedad terrestre, en los árboles por ejemplo; es un esfuerzo por alcanzar la luz del sol, tal como en la arquitectura gótica, donde aparecen las estrellas de cinco puntas en sus trazados compositivos.
El científico alemán Zeysing reencontró esta divina proporción en 1850, declarando: «Para que un todo, dividido en partes desiguales parezca hermoso desde el punto de vista de la forma, debe haber entre la parte menor y la mayor, la misma razón que entre el mayor y el todo». A esto lo llamó «ley de las proporciones», encontrando su presencia en numerosas plantas y flores, en los animales que se distinguen por la elegancia de sus formas, en el cuerpo humano, en las obras de arquitectura antigua y en música.
En botánica, Zeiysing descubre que los ángulos que se forman en las ramas de los árboles a medida que van creciendo en hélice, tenían en promedio un valor de 137º30’28” = 360º/ Ф².
Este ángulo coincide con el ángulo constante que deben tener entre sí las hojas o las ramas de una planta, tomando como centro el eje del tronco, de tal manera que se asegure el máximo de exposición a la luz vertical y para que sus proyecciones horizontales no se recubran totalmente. El pentágono está presente en numerosas flores, especialmente en las de árboles frutales, como el manzano, la fresa, el nenúfar amarillo. Se puede observar en el pedúnculo de los tomates o en la sección ecuatorial de una manzana.
La serie de Fibonacci
La serie de Fibonacci también hace su aparición entre las plantas, como diagrama de crecimiento. En la distribución de los granos, así como de las hojas, se encuentra esta serie, que está emparentada con la sección áurea. En el girasol, por ejemplo, se observa en su frente un disco plano dividido en pequeños rombos por las intersecciones de dos grupos de curvas, que son precisamente dos espirales logarítmicas, derivadas de la serie Fibonacci. Lo mismo ocurre con las piñas de las coníferas, y gran variedad de flores y frutos.
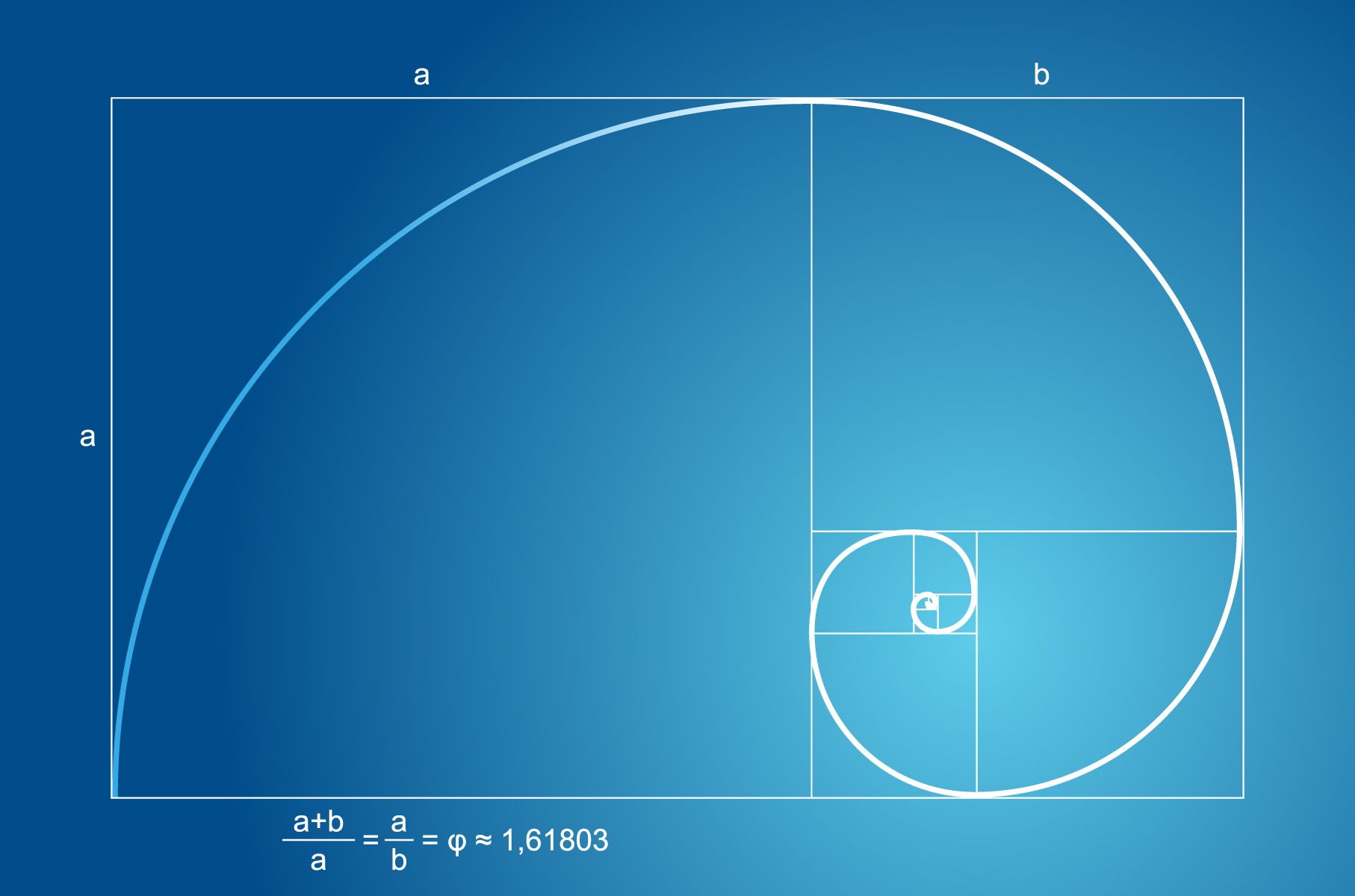
Siguiendo la línea marcada por la curva, toda espiral o fragmento de esta, puede evocar una ley de crecimiento, una pulsación rítmica, que aparece también en numerosas conchas y esqueletos de organismos marinos, en los caracoles, en los cuernos de algunos mamíferos.
Como afirma D’Arcy Thompson en su libro Crecimiento y forma , citado por Matila Ghyka: «La concha retiene su forma inmutable, a pesar de su crecimiento asimétrico y, lo mismo que los cuernos de los animales, crece solo por una extremidad. Esta notable propiedad de aumentar por crecimiento terminal sin modificación de la forma de la figura total, es característica de la espiral logarítmica y no la tiene ninguna otra curva matemática». Se pueden construir numerosas espirales en progresión geométrica, pero al parecer, la naturaleza elige para los organismos vivos aquellas espirales en las que sus radios están en progresión Ф.
También es importante mencionar aquí la catenaria como curva natural, que forma una cuerda apoyada en sus dos extremos, de la cual se sirven las plantas y los árboles, por su efectiva resistencia y que el gran arquitecto Antonio Gaudí supo observar y utilizar en sus estructuras. Esta curva, que se acerca a la parábola, es el resultado de un estado de equilibrio consecuente con el principio de mínima acción. Si lo invertimos, es el arco donde se encuentra más bajo el centro de gravedad.
Una curva es capaz de engendrar, por su giro en torno a un eje dado, una superficie mínima. Es justamente el perfil de un huevo. Se trata de una obtusa y la otra más aguda que se unen en un foco, de manera que son dos catenarias de longitud diferente. Según los estudios de D’Arcy Thompson, habría dos tipos de formas de huevo: uno se inscribe en un rectángulo de razón Ф, y el otro en uno de razón √Ф. El círculo donde más se ensancha el huevo, que está más cerca del casquete más aplastado, divide el eje longitudinal según la sección áurea.
Animales y humanos
En los cuerpos de los animales se encuentra la divina proporción, como por ejemplo en las patas delanteras de los caballos. La morfología de los insectos presenta una variedad de relaciones asimétricas que se basan en la serie Ф. En el reino animal se observan formas pentagonales o derivadas del pentágono, como es el caso más evidente de las estrellas de mar y otro gran número de conchas. La pentadactilia es el fenómeno de poseer cinco dedos en las extremidades, lo cual es común al hombre y a muchas especies animales, como se ve en la estructura de la aleta de la ballena. De hecho, en la mayoría de animales, especialmente en los mamíferos, del tronco surgen cuatro extremidades y la cabeza, siguiendo formas que derivan del pentágono.
Sir Theodore Cook, en su libro The Curves of Life , compara el crecimiento de los seres en la naturaleza con las obras de arte, admitiendo el carácter rigurosamente matemático de las leyes de formación y desarrollo, pero observa también que las curvas tienen ligeras oscilaciones con respecto a los modelos teóricos, y que son estos tanteos una de las características importantes de la vida, del encanto de las formas, algo muy similar a lo que ocurre con las obras de arte. Hay un elemento imprevisto, que no se puede predecir en un laboratorio científico y que hace que los diferentes organismos sean mucho más que una máquina predeterminada.

El ser humano también está dentro de este universo y está regido por sus leyes, aunque a veces actuemos como si no perteneciéramos a él. La sección áurica se encuentra en el cuerpo humano, como ya ha sido estudiado y sabido desde la Antigüedad; prueba de ello son las esculturas griegas. En esas obras, así como en personas bien proporcionadas, el ombligo divide la altura total según la divina proporción, tal como estudiaron en el Renacimiento Durero y Leonardo da Vinci. Sin embargo, en los diferentes cuerpos se aprecian oscilaciones. Zeysing, tras un extenso estudio comparativo, observa en los cuerpos sanamente desarrollados la tendencia a la razón Ф.
No obstante, encuentra proporciones diferentes entre cuerpos masculinos y femeninos. En los hombres, al dividir la altura total por la altura hasta el ombligo, halló una oscilación alrededor de la razón 13/8 = 1,625, mientras en la mujeres se oscilaba alrededor de 8/5 = 1,6.
Aquí se habla de cuerpos en edad adulta. Zeysing hace un estudio desde el nacimiento de un ser humano, y cómo varían sus proporciones al crecer. Lo interesante de estos resultados en la edad adulta es que ambas razones están conformadas por números que forman parte de la serie de Fibonacci, donde como se había ya mencionado, los coeficientes de dos números consecutivos tienden rápidamente a Ф. La serie es 1,1,2,3,5,8,13,21,44…
También en otras partes del cuerpo está la sección áurea. La cabeza humana se puede encuadrar en un rectángulo áurico. Si se divide la altura del rostro por la longitud del mentón al arco de las cejas, o si se divide la distancia de la punta de la nariz al mentón entre la que hay de la comisura de los labios al mentón, se obtienen aproximaciones a Ф. En la falange de los dedos índices se halla esta proporción en tres términos consecutivos, donde el tramo mayor es igual a la suma de los otros dos.
Aún se podría detallar más el análisis del cuerpo humano. Para no entrar en demasiados detalles, se menciona a continuación la obra del estadounidense Jay Hambidge, publicada en 1919. Inspirado en un pasaje del Teeteto de Platón, sobre números y longitudes conmensurables en potencia, y al no encontrar una formulación clara para los trazados de los templos y las obras de arte antiguas, en las que se presumían unas proporciones, pero en las que la aplicación de la sección áurea de manera lineal no satisfacía, tuvo la idea de estudiar estos trazados, no en líneas sino en superficies y volúmenes, algo que es más propio de las artes plásticas. También estudió el cuerpo humano, y más propiamente el esqueleto, estableciendo una teoría de proporciones más flexible, donde se encuentra, con más precisiones, una serie de «razones dinámicas». Pudo comprobar en diferentes esqueletos, vistos de frente y de perfil, un ritmo armónico de rectángulos, donde predominan los de módulos irracionales como √5 y Ф, encontrándose también una sinfonía dinámica característica, basada en un esquema riguroso.





















