
El 14 de marzo se celebra el día del número pi (π), la constante que indica la relación entre la longitud de una circunferencia y su diámetro. Esta fecha, en clave numérica, y poniendo primero el número del mes, se representaría como 3-14, que nos recuerda a las primeras cifras del número pi, que solemos mencionar como 3.1416.
El origen de esta celebración se remonta a 1988, cuando se empezó a conmemorar en el Museo de Ciencias de San Francisco, el Exploratorium. En 2009, el Congreso norteamericano instituyó el Día Internacional de π, y desde hace pocos años también lo celebramos en España, promovido por la Real Sociedad Matemática Española.
Aunque lo simplifiquemos con «tres catorce dieciséis», en realidad no se conoce con exactitud cuál es su valor, porque tiene una cantidad infinita de decimales, empezando por 3.14159265358979323846…
Una de sus características más significativas es que pi es «irracional» y no puede expresarse como la división de números enteros (números sin decimales). Por eso, π no solo tiene infinitas cifras decimales, sino que no se repiten periódicamente. Además, pi es también «trascendente», pues no es solución de ninguna ecuación algebraica con coeficientes racionales (como lo es, por ejemplo, la raíz cuadrada de dos = 1.414213…).
Pi no solo relaciona la longitud de una circunferencia y su diámetro (πd), o el área de un círculo y su radio ( ), sino que interviene en otros aspectos matemáticos, como en las oscilaciones [1] , en la probabilidad [2] , en series infinitas [3] , o en otros que podemos llamar casualidades [4] . Y por supuesto hay que mencionar la más bella ecuación matemática, la de Euler e iπ + 1 = 0, que relaciona los cinco números más importantes en matemáticas: 0, 1, i, π y e, donde i es la raíz cuadrada (imaginaria) de -1, y e es el número de Euler o constante de Napier, usado para el cálculo de los logaritmos.
Además, y esto puede resultar lo más sorprendente para el lector, al tener un número infinito de cifras, en su desarrollo se puede encontrar cualquier secuencia que queramos: nuestra fecha de nacimiento, el número de nuestro móvil, o la cantidad de palabras de este artículo y la hora exacta en que usted lo está leyendo.
Por tener infinitos decimales y una distribución totalmente aleatoria se ha utilizado en numerosos cálculos y simulaciones matemáticas. A esta característica se la conoce en matemáticas como «normal»: un número normal es aquel en el que todos sus dígitos están uniformemente distribuidos, es decir, todos los números de una cifra aparecen con la misma frecuencia, todas las parejas de dos cifras aparecen también con igual frecuencia, e igualmente con los de tres cifras, los de cuatro, etc. No se ha podido comprobar la «normalidad» de las cifras de pi, pero hasta ahora los cálculos que se han realizado apuntan a esta propiedad.
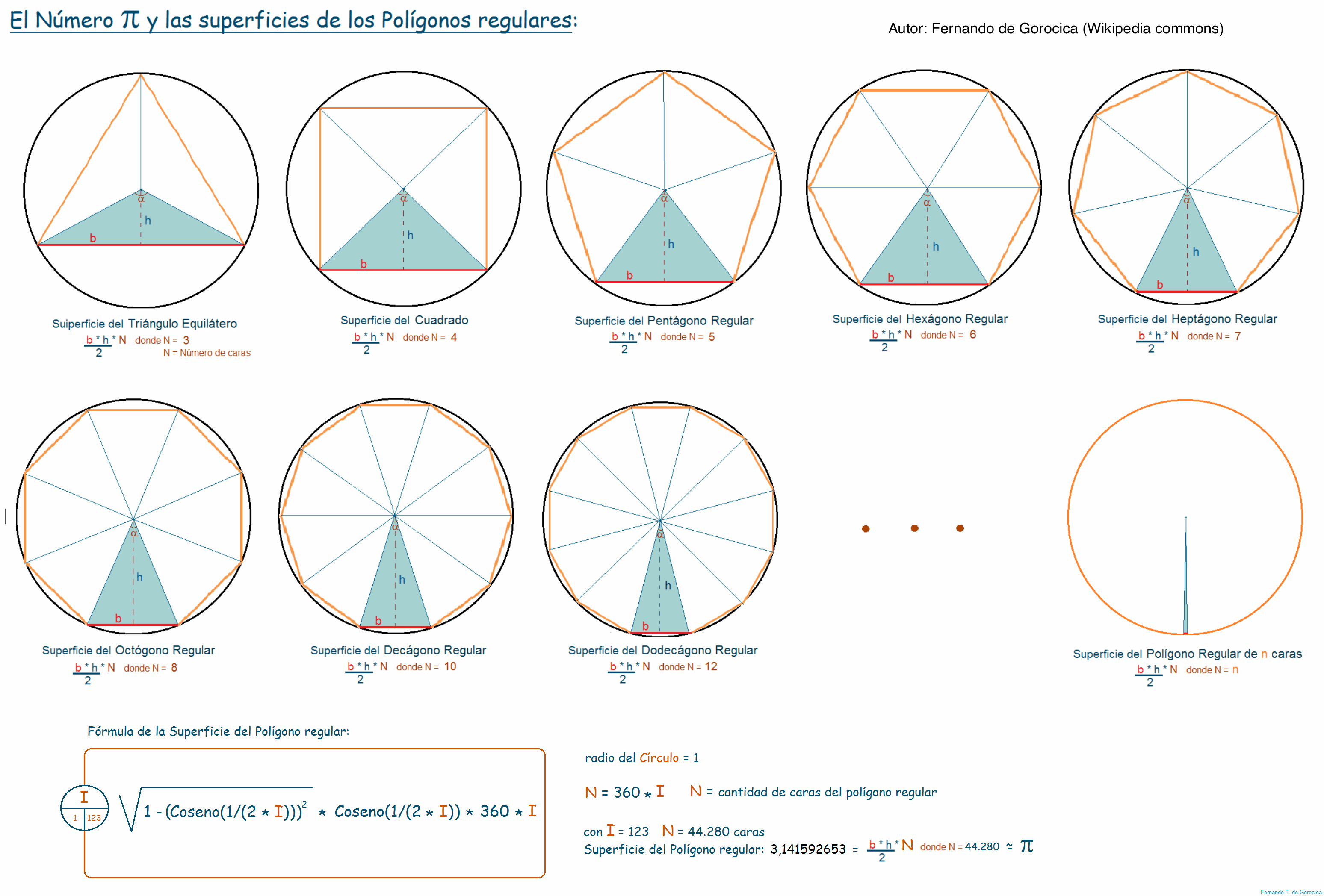
Uno de los retos matemáticos desde la Antigüedad [5] ha sido determinar más cifras de su desarrollo decimal. Esto ha servido para progresar en los métodos de cálculo que, por ejemplo, utilizan ahora las computadoras más avanzadas a la hora de resolver ecuaciones por medio de aproximaciones.
Pi también aparece en la fórmula de la transformada de Fourier, que sirve para separar las series temporales constitutivas de una señal. Esta separación la usamos sin darnos cuenta, por ejemplo, para reconocer la voz de un amigo entre un conjunto de voces. La usa nuestro teléfono móvil para conectarse a una antena de nuestro proveedor telefónico. O también lo usan los asistentes de voz para la conversión de voz a texto inteligible.
Pi aparece también en los GPS, no solo los que tiene nuestro teléfono móvil para la orientación en pequeñas distancias, sino incluso en los cálculos de los aviones o de los satélites espaciales. De hecho, la NASA utiliza hasta el decimosexto decimal de pi (3.1415926535897932) para la precisión de sus cálculos.
[1]
[1] Cuando un péndulo se balancea adelante y atrás, la posición se comporta como una coordenada de una partícula que rodea un círculo. Si su desplazamiento máximo es de un metro y su velocidad máxima es de un metro/segundo, su período de oscilación será exactamente de 2π segundos.
[2]
[2] La probabilidad de que una aguja lanzada sobre un papel, en el que haya dibujadas unas líneas paralelas separadas entre sí una distancia igual a la longitud de la aguja, cruce alguna de dichas líneas es igual a 2/π.
[3]
[3] La suma infinita de las áreas de cuadrados de lados 1,1/2, 1/3, …, 1/n es igual a π2/6. Expresado algebraicamente sería 12 + (1⁄2)2 + (1⁄3)2 + (1⁄4)2 + ( 1⁄5)2 + ⋯ = π2/6. Otra sucesión infinita que también se aproxima a pi es 1 –1⁄3 + 1⁄5 –1⁄7 + 1⁄9 + ⋯ = π/4.
[4]
[4] Por ejemplo, la duración de un año terrestre en segundos es aproximadamente de diez millones por el número pi, y no tiene nada que ver con la órbita casi circular de la Tierra. Hay otra serie de «coincidencias» que algunos aficionados a las matemáticas mencionan, obviando que son aproximaciones: la relación entre pi y Phi, π≈4/√φ, siendo φ el «número de oro», o la relación entre pi y la raíz de 2, π ≈ (14-√2)/4. Sin mencionar las supuestas relaciones geométricas con la altura de las pirámides de Guiza o con el área de la base.
[5]
[5] Los babilonios usaron la aproximación pi ≈ 3 y posteriormente usaron 3 1/8 = 3.125. El papiro egipcio de Rhind, fechado aproximadamente en 1650 a. C., sugiere π ≈ 256/81 = 3.16049. Los primeros matemáticos indios creían que π ≈ √10 = 3.162277. El matemático y filósofo griego Arquímedes, en el primer cálculo matemáticamente riguroso de pi, empleó una construcción iterativa inteligente de polígonos inscritos y circunscritos para establecer que 223/71 < π < 220/70. Es decir 3.14084 < π < 3.14285. Una de las mejores y más sencillas aproximaciones, utilizado parejas de los primeros números impares es π ≈ 355/113 = 3.14159292.





















