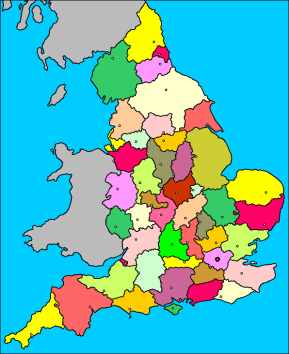
¿Sabéis cuál es el problema más fácil de enunciar y más difícil de resolver de todas las matemáticas? Es el llamado problema de los cuatro colores, planteado en 1852, y surgió tratando de colorear los diferentes condados de un mapa de Inglaterra. Se enuncia así:
¿Se puede colorear cada zona en que aparece dividido un mapa con uno de cuatro (o menos) colores, de tal forma que no haya dos zonas con frontera común que tengan el mismo color?
La respuesta positiva es una demostración tediosa que requiere de varios miles de horas utilizando un ordenador rápido. ¿Existe alguna demostración más sencilla? Nadie lo sabe todavía. Se han intentado diferentes tipos de demostraciones, por ejemplo la demostración por reducción al absurdo –suponer que el teorema es falso y llegar a una contradicción–. Pero este teorema no sucumbe tan fácilmente.
En 1950 Heinrich Heesch afirmó que el teorema se podía demostrar hallando un conjunto inevitable de configuraciones reducibles (que se puedan a su vez reducir a triángulos, cuadrados, pentágonos, donde sí es positiva la demostración del teorema). Heesch y su discípulo Karl Dürre crearon un programa de ordenador para realizar la prueba de reductibilidad. Pero no fue infalible. Si una configuración superaba la prueba, era reducible; pero si la prueba daba negativo, quedaba sin determinar si era reducible o no.
La demostración vino de la mano de Appel y Haken y un programa de ordenador que comprobaba todas las configuraciones de un conjunto inevitable. Fue en 1976, como corona de un esfuerzo de diez años y muchos colaboradores.
Si la demostración se fuera a escribir, sería tan larga que nadie viviría el tiempo suficiente para leerla, y por tanto, para poder asegurar que en ella no hay ningún fallo. Entonces, ¿por qué los matemáticos están convencidos de que la demostración es correcta? Porque la estrategia es correcta, los detalles no se contradicen entre sí, nadie ha encontrado un error grave, y además, como dijo Haken:
«El hecho de que el ordenador pueda en unas pocas horas tratar más detalles que los que un ser humano podría trabajar en toda su vida, no cambia el concepto básico de demostración».
Así también, aunque las demostraciones en los estudios filosóficos a través de los siglos sobre cómo ser feliz no son concluyentes, seguimos convencidos de que una vida ética es el camino para una vida feliz.
También te puede interesar:
Spanish